Strukturgleichungsmodelle lassen das Herz jedes Statistik-Fans höherschlagen. Doch welchen Erkenntnisgewinn bringen sie der angewandten Marktforschung? Und was ist bei ihrem Einsatz zu beachten? Ein Überblick.

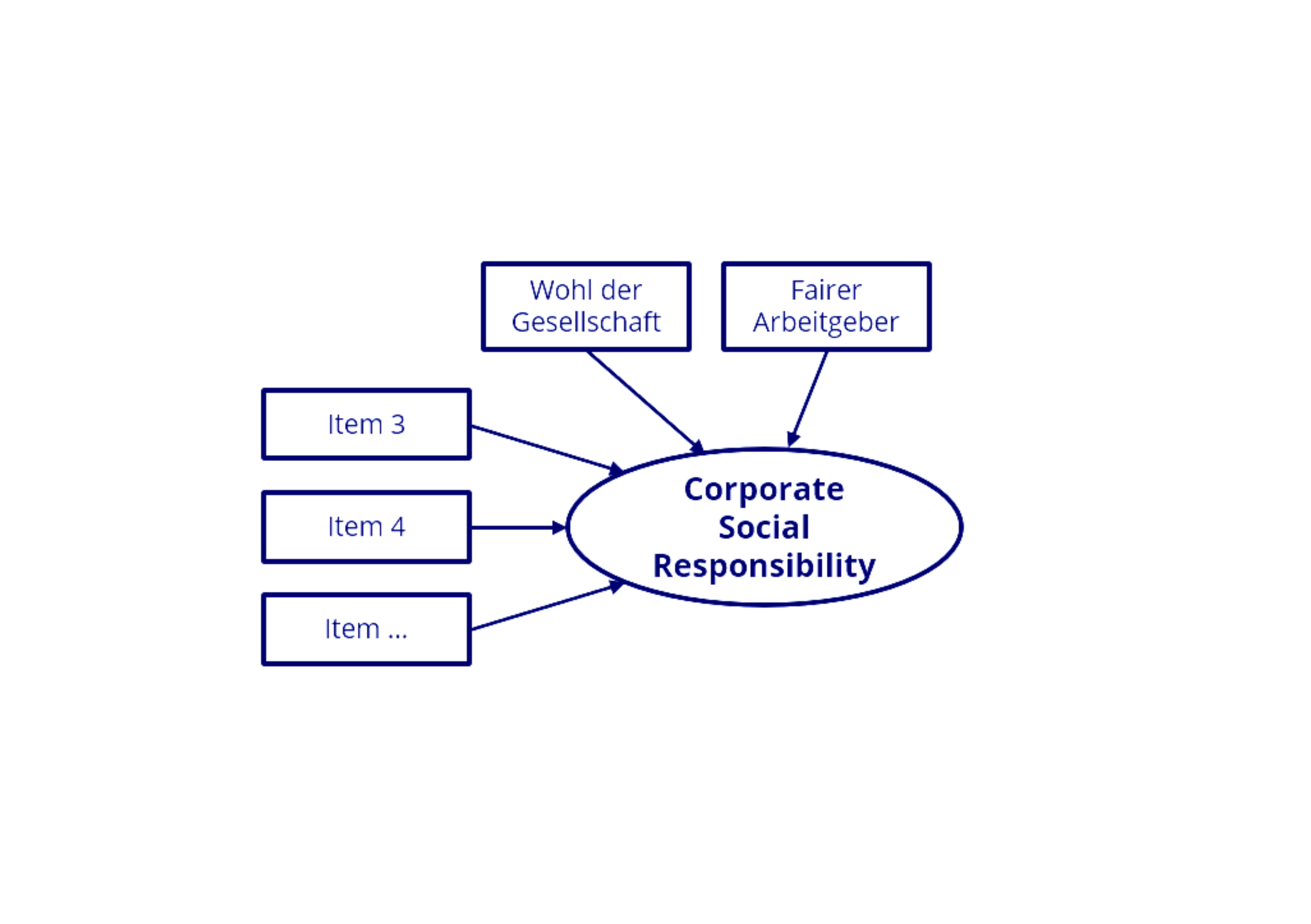
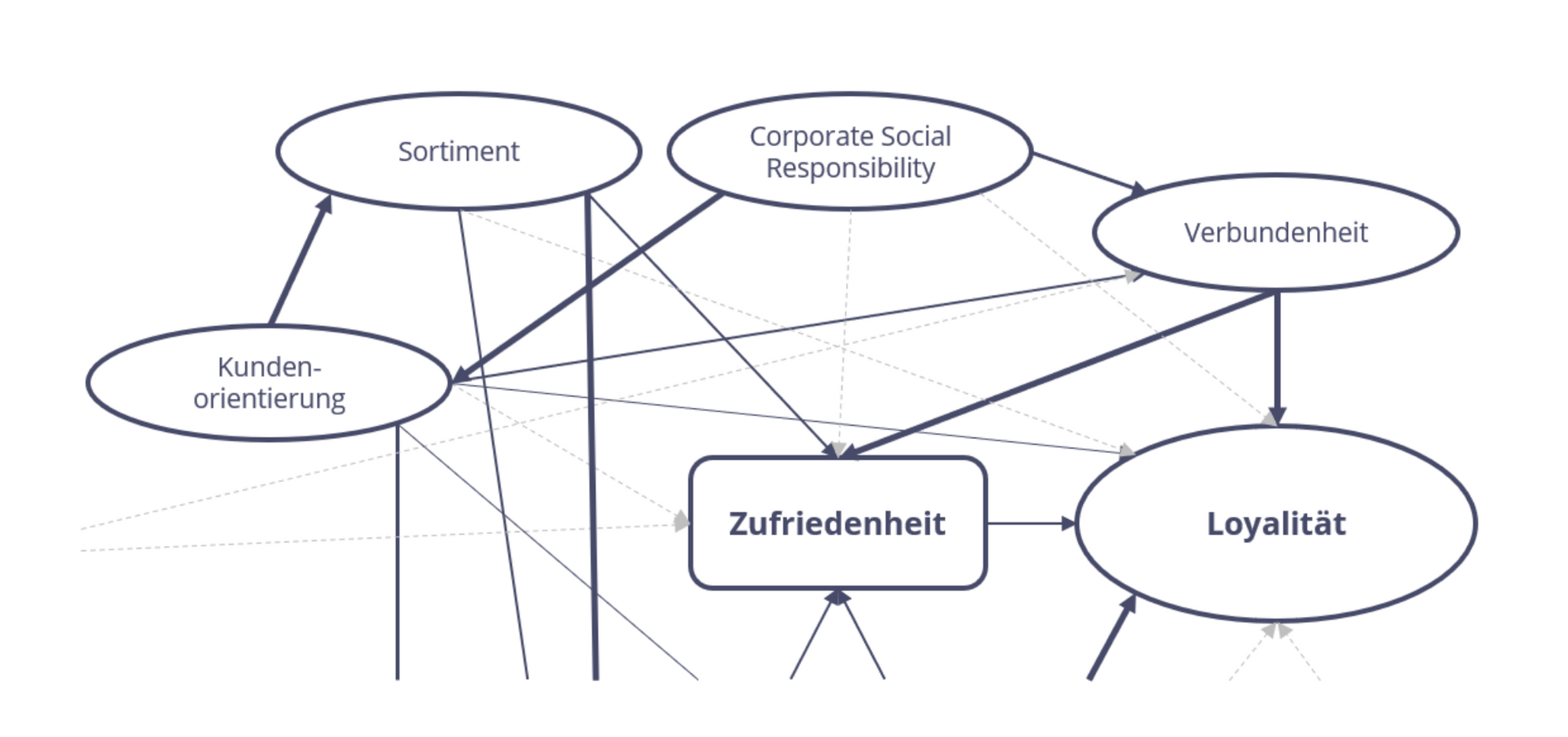
Mittwochmorgen, 10.24 Uhr: Eine neue Anfrage eines langjährigen Kunden trifft im E-Mail-Postfach ein: Er möchte untersuchen, welche Faktoren die Zufriedenheit seiner Kund:innen beeinflussen und ihre Loyalität gegenüber seiner Marke massgeblich prägen. Spannend, denken wir – und möglicherweise gar nicht so einfach zu beantworten, wie man es auf Anhieb erwarten könnte. Ein erstes Gespräch mit unserem Kunden bestätigt diesen Eindruck: Es kristallisiert sich heraus, dass die interessierenden Zusammenhänge komplex sind und anhand einfacher multivariater Analysemethoden (z. B. einer Regressionsanalyse) nur unzureichend modelliert werden können. Zudem wissen wir aus Erfahrung, dass einige der Konstrukte, die unseren Kunden interessieren – z. B. Kundenorientierung oder Corporate Social Responsibility – nicht direkt messbar sind, sondern über mehrere einzelne Fragen erhoben werden sollten. Um die vermuteten Wirkzusammenhänge adäquat abbilden und allenfalls sogar Zusammenhänge entdecken zu können, die so im Vorfeld nicht absehbar sind, bieten wir unserem Kunden ein Forschungsdesign an, das auf einem Strukturgleichungsmodell aufbaut. Doch was sind Strukturgleichungsmodelle genau und wann kommen sie sinnvollerweise zum Einsatz?

Im Falle unseres Kunden sind alle Voraussetzungen für den Einsatz eines Strukturgleichungsmodells gegeben. Doch häufig gibt es auch gute Gründe, auf ein Strukturgleichungsmodell zu verzichten:

• Zum einen stellt ein Strukturgleichungsmodell höchste Ansprüche an die Datenqualität: Jedes verwendete latente Konstrukt wird durch mehrere (mindestens drei) passende EinzelItems abgebildet. Diese müssen anhand entsprechender Modellierungen darauf geprüft werden, ob sie das Konstrukt ausreichend gut beschreiben. Die Messmodelle der einzelnen Konstrukte müssen anschliessend ebenso wie das Strukturmodell als Ganzes einer eingehenden Prüfung auf diverse Kriterien unterzogen werden. Erst wenn alle Kriterien erfüllt sind, kann ein Modell als gut bezeichnet und interpretiert werden. Erhebt man die Daten selbst oder lässt sie wie im Falle unseres Kunden durch ein mit der Materie vertrautes Befragungsinstitut erheben, so können diese Aspekte bereits in der Konzeptionsphase adressiert werden. Arbeitet man hingegen mit Sekundärdaten, so kann dies durchaus zu einer Herausforderung werden. Ein theoriebasiertes Vorgehen bei der Erarbeitung des Strukturgleichungsmodells und seiner einzelnen Komponenten ist in beiden Fällen unabdingbar.
• Zum anderen ist ein Strukturgleichungsmodell auch nicht in jedem Fall die geeignetste Methode: Häufig können die interessierenden Zusammenhänge auch mit einfacheren statistischen Verfahren wie zum Beispiel einer Regressionsanalyse gut analysiert werden. Die Komplexität von Strukturgleichungsmodellen bringt mit sich, dass diese nur von Expert:innen – notabene mithilfe spezieller Software – gerechnet und interpretiert werden können. Entsprechend höher sind auch die benötigten zeitlichen und personellen Ressourcen. Im konkreten Fall sollte daher immer ausgehend von der konkreten Fragestellung und gemeinsam mit Expert:innen entschieden werden, welches Vorgehen am sinnvollsten ist.

Doch zurück zu unserem Kunden: Für ihn hat sich der Entscheid, ein Strukturgleichungsmodell rechnen zu lassen, definitiv gelohnt! Dieses hat nämlich gezeigt, dass die Corporate Social Responsibility – ein latentes Konstrukt, das über zehn Einzelfragen erhoben wurde – zwar keinen direkten Effekt auf die Loyalität hat, diese über andere Konstrukte (z.B. die Verbundenheit) aber indirekt dennoch deutlich prägt. Diese Effekte hätte eine klassische Regression nicht aufdecken können, da sie keinen vollständigen Wirkungsmechanismus mit verschiedenen Wirkungspfaden auf verschiedene Konstrukte berechnen kann. Dank des Strukturgleichungsmodells konnte der Einfluss der Corporate Social Responsibility auf die Loyalität nachgewiesen werden.

Eine vertiefte Auswertung einzelner Treiber der Corporate Social Responsibility brachte zudem weitere interessante Ergebnisse zutage: So konnte aufgezeigt werden, dass die drei Einzelaspekte «Fairness gegenüber Wettbewerbern», «Fairer Arbeitgeber» und «Beitrag zum Wohl der Gesellschaft», die das Konstrukt Corporate Social Responsibility im Kern ausmachen, zwar überdurchschnittlich wichtig für die Loyalität der Befragten gegenüber dem Kunden sind, von ersteren aber bislang unterdurchschnittlich bewertet wurden. Dank dieser Analyse, die wiederum alle direkten und indirekten Effekte einbezog, kennt unser Kunde nun diejenigen Aspekte, die das grösste Verbesserungspotenzial haben. Basierend auf diesen Erkenntnissen kann er konkrete Ideen zur Steigerung der Loyalität erarbeiten und Massnahmen im Bereich Corporate Social  Responsibility gezielt vorantreiben.

Grafik 3: Auszug aus einem Strukturgleichungsmodell

intervista verfügt über umfassende Erfahrung und Expertise rund um Strukturgleichungsmodelle und weitere multivariate Analysemethoden. Wir setzen Strukturgleichungsmodelle in verschiedenen Bereichen erfolgreich ein, so zum Beispiel in der Werbewirkungsforschung oder in Kundenzufriedenheits- und Imagestudien. Zusätzlich bieten sich Strukturgleichungsmodelle dann an, wenn ein allgemeines Verständnis von Wirkungsabläufen etabliert oder geprüft werden soll. Möchten auch Sie von unserer Erfahrung und Expertise rund um Strukturgleichungsmodelle und weitere multivariate Analysemethoden profitieren? Melden Sie sich bei uns, wir beraten Sie gerne!